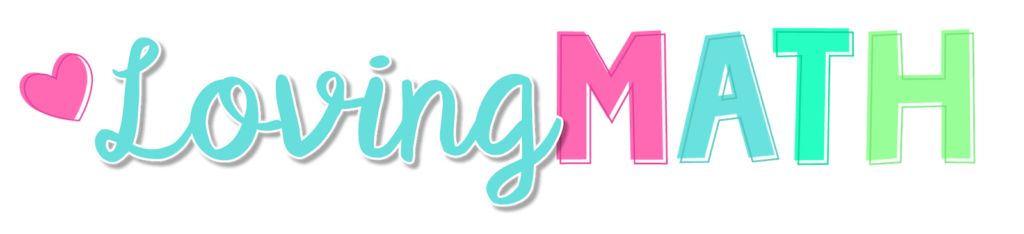Many US students have a weak understanding of fractions. The biggest complaint I hear from teachers everywhere is ” My students lack fraction fluency”.

Here are some stats from The National Assessment of Educational Progress (NAEP) :
- 50% of 8th-graders could not order three fractions from least to greatest (NCTM, 2007)
- Fewer than 30% of 17-year-olds correctly translated 0.029 as 29/1000
- One-on-one controlled experiment tests – when asked which of two decimals, 0.274 and 0.83 is greater, most 5th- and 6th-graders choose 0.274 (Rittle-Johnson, Siegler, and Alibali, 2001)
Why do so many students lack fraction fluency?
Many students and teachers don’t think of fractions as numbers. They think of fractions as something very abstract that has no use in the real world.
In its report, the National Math Panel said the failure to master fractions was for American students the greatest obstacle to learning algebra.
It is the role of elementary school teachers to set the foundation for understanding fractions in order to build fraction fluency.
Here are some ideas to follow when introducing fractions to students and covering the fractions chapters:
1. Fractions are Numbers
The Common Core standards define fractions as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b. They also define fractions as a number on a number line.
When teaching fractions, don’t solely focus on the “pizza” model. Use fractions in daily conversations with your students. Fractions are numbers after all.
Some ideas to talk about fractions daily with your students:
- Attendance: When taking attendance mention the fraction of students that is present and absent.
- Time: When discussing the daily schedule or how much time is left for lunch. For example: “We go to lunch at 12:00 noon and it is now 11:45 am. We have 1/4 of an hour left until we go to lunch”
- Grades: “Boys and girls, 4/5 of the class scored above 90 on our last test. We have 20 students in the class, so that is 16 students.”
- Counting: We teach our students to count by 1s, by 2s, by 5s, backwards. So, why not count by fractions. Draw the number lines as you count and make those connections to fractions as whole numbers, comparing, and so forth. This could be a daily morning meeting activity with lots of math talk. Let them talk about it and notice the misconceptions..
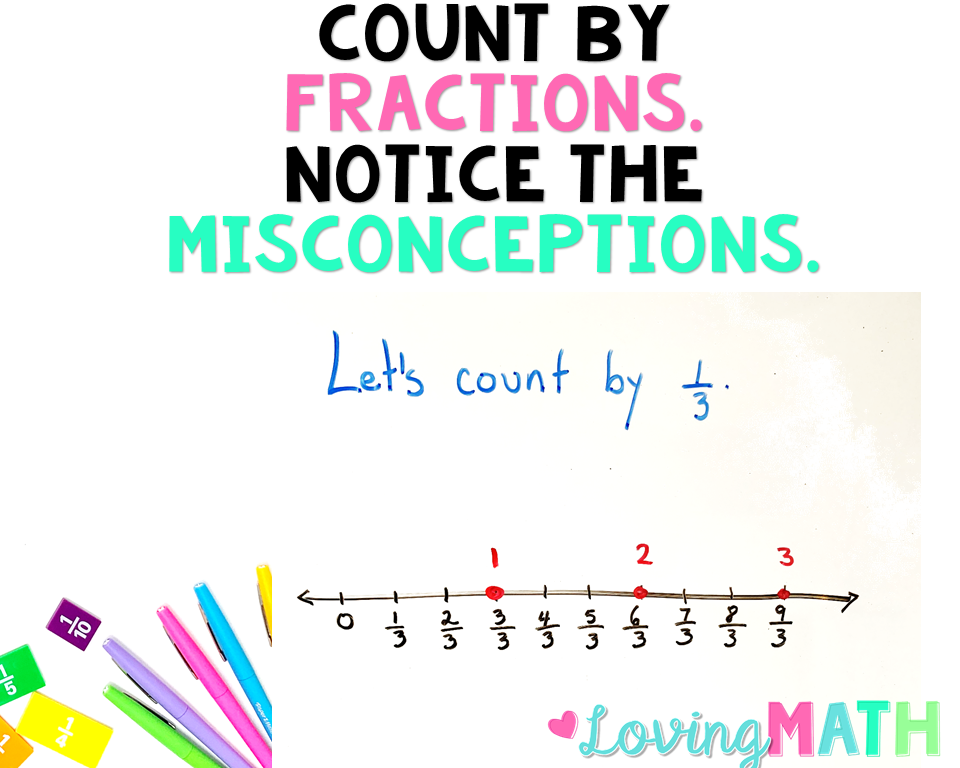
2. Use concrete models
I believe most teachers do this. In my role as a math coach, I often see students using fraction tiles or circles when fractions are being introduced. The problem I see is that many teachers only use them a handful of times. The reason? They are messy, noisy, and kids just play with them.
But please note that this is an important step in gaining mastery of fractions. If you want your students to improve fraction fluency, concrete models are a must.

I vividly remember my now teenage son when he was in his early elementary years learning fractions. One day he was doing homework and had to compare 2 fractions. The fractions he was comparing escapes me but I remember he quickly was able to tell me which ones were greater. When I pressed him to explain how he knew without drawing or using models he replied ” I have memorized the fraction tiles, I know the fourths are greater than the fifths so if I have 2/4 it is definitely greater than 2/5.
His teacher had done a great job letting them play with those models. He had memorized the colors of the tiles and had come to analyze them in great detail.
So, let the kids play, build things, or point the tiles at one another. They are learning and cementing the understating of these numbers.
3. Number Lines are Key
When teaching fractions and aiming for fraction fluency, number lines are essential.

Help students recognize that fractions are numbers and that they expand the number system beyond whole numbers. Use number lines as a central representational tool in teaching this and other fraction concepts from the early grades onward.
- Use measurement activities and number lines to help students understand that fractions are numbers, with all the properties that numbers share.
- Provide opportunities for students to locate and compare fractions on number lines.
- Use number lines to improve students’ understanding of fraction equivalence, fraction density (the concept that there are an infinite number of fractions between any two fractions), and negative fractions.
- Help students understand that fractions can be represented as common fractions, decimals, and percentages, and develop students’ ability to translate among these forms.
- Use plenty of open ended problems where students have the opportunity to explain their thinking.
4. Help students understand why procedures for computations with fractions makes sense.
- Use area models, number lines, and other visual representations to improve students’ understanding of formal computational procedures.
- Provide opportunities for students to use estimation to predict or judge the reasonableness of answers to
problems involving computation with fractions. - Address common misconceptions regarding computational procedures with fractions.
- Present real-world contexts with plausible numbers for problems that involve computing with fractions.

4. Get Professional Development
Professional development programs should place a high priority on improving teachers’understanding of fractions and of how to teach them.
- Build teachers’ depth of understanding of fractions and computational procedures involving fractions.
- Prepare teachers to use varied pictorial and concrete representations of fractions and fraction operations.
- Develop teachers’ ability to assess students’ understandings and misunderstandings of fractions.
Here are some resources you might be interested in to build fraction fluency with your students:
Fraction Sort Game Comparing Fractions
Line Plots with Fractions Practice Problems